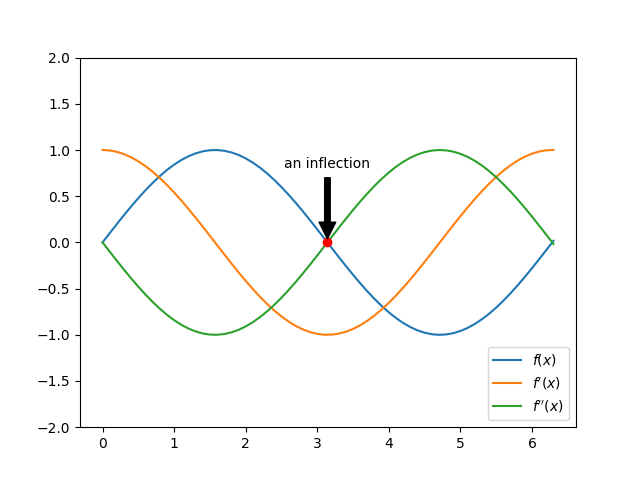
二阶导数描述凹凸性和拐点

Concavity 凹凸性

inflection 拐点

This is a part graph about $f(x)=e^x$

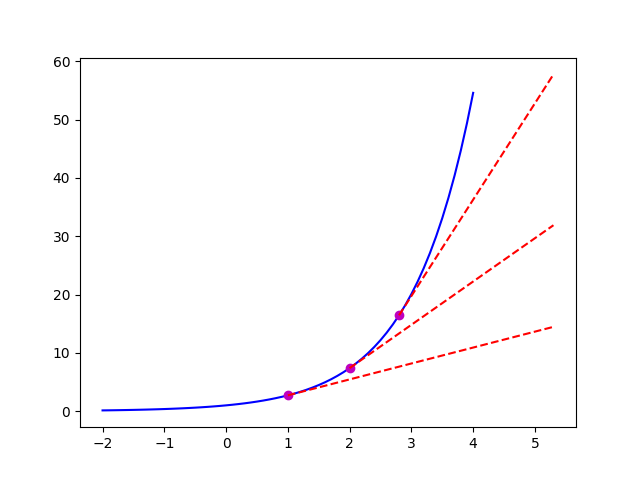
Every red line's slop represented as a certain first derivative $f^\prime(x)$.

You can see it clearly that it indeed goes steeper and steeper, $f^\prime(x)$ gets bigger and bigger.

That means $f^\prime(x)$ keep increasing in this interval.

So according to the first derivative theory, $f^{\prime\prime}(x)$ must be positive.

For a function interval has a feature of $f^{\prime\prime}(x) > 0$, we call it concave upwards (凸).

This is a part graph about $f(x)=-x^2$

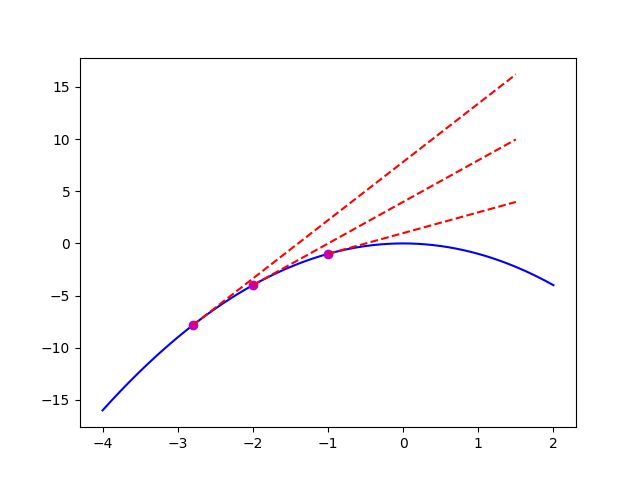
Every red line was becoming more and more gentle, $f^\prime(x)$ gets smaller and smaller.

That means $f^\prime(x)$ keep decreasing in this interval.

So according to the first derivative theory, $f^{\prime\prime}(x)$ must be negative.

For a function interval has a feature of $f^{\prime\prime}(x) < 0$, we call it concave downwards (凹).

$f^\prime(x)$ first decreasing , then increasing, you'll get an inflection

$f^\prime(x)$ first increasing, then decreasing, you'll also get an inflection